
|
 |
|
Bumps In The Road by Brian Beckman PhD and Jerry Kuch
This month, we investigate how the effects of road bumps vary with speed. Everyone has experienced that bumps are more punchy as speed
increases. A bump that you barely notice at 50 mph can sting at 100 mph. But what about at 200 mph? Will it just smack a little
harder, or will it knock your teeth out or, worse, cause you to lose control? Could a bump be the limiting factor in cornering speed?
In an aerodynamic car, could a bump cause a sudden and catastrophic loss of downforce and adhesion? To analyse such things, we need
an understanding of the variation of bump violence with speed.
At the expense of a little storytelling, let's explain how this topic came up. In particular, where is an amateur motorhead going to have to worry about bumps at 200 mph? At autocrosses, speeds are low, by design, to give everyone a safe venue to challenge the limits. If you're going to spin out, an autocross is the place to do it. Low speed also means, though, that bumps, unless very severe, aren't dominant. On a road course, speeds are higher, as are the consequences of losing control. But speeds are not higher everywhere, not for extended times, and seldom approach 200 mph. There are two commonplace scenarios with extended time at high speeds: oval courses and open-road racing. High-speed oval racing is a specialized sport not often encountered by amateurs. Since the focus of this series is on grassroots, amateur hijinks, we'll look at open-road racing. In Part 11 of this series, we took a scenario for braking from 200 mph from the Silver-State Challenge (SSC) in Nevada. My co-author, Jerry Kuch, and I just ran the 2000 Nevada Open Road Challenge (NORC). This is the May version of the SSC, which is held in September. In all other regards, the NORC and the SCC are the same. For most of the 230 cars entered, these are high-speed, time-speed-distance (TSD) rallies. In each of the sixteen TSD classes, the car running as close as possible to the target speed, over or under, wins. There are TSD classes every five mph from 95 to 170 inclusive, with high and low breakout speeds set by safety concerns. There is also an Unlimited, non-TSD class, in which fastest car wins. This May, the winner of Unlimited averaged 207 mph over a ninety-mile distance and another Unlimited car posted a top speed of 227 mph. Jerry and I ran in the 130-mph class with a top speed of 165 mph. The SCC and NORC run on a ninety-mile stretch of highway 318 from Lund to Hiko in the Nevada outback, roughly along the shortest path from Twin Falls, ID to Las Vegas. The course runs from north to south, and the road is fabulously stark and beautiful in the unique way of remote desert roads. One is humbled by the realization that if stranded, one would surely perish, probably in a few hours' time, from heat exhaustion, exposure, and dehydration. It's great. Hwy 318 events have been run continuously on since 1988. In 1990 and 1991, Mark Thornton, a fellow autocrosser, built up his 1986 Super Stock corvette into a Nevada car. Mark and I had nearly identical SS 'vettes, and we often swapped cars at autocrosses. These cars happened to be almost the same as the famous yellow 'vette that Roger Johnson, of multiple SCCA National Championships, still runs in SS, if I'm not mistaken. I know that Roger has driven my car, and I can't recall whether he ever drove Mark's, but I did, many times. Mark, now deceased, was a bit of a bad boy, and Hwy 318 had just the kind of cachet that appealed to him. The legend goes that the events had been organized by the survivors of the old, illegal 'cannonball' runs. Of course, the NORC and SCC are properly sanctioned and completely legal, despite the fact that they use temporarily closed public highways rather than dedicated race courses. Not content to play in the TSD classes, Mark decided to convert the black car into an Unlimited machine. I was with Mark when he handed his car off to Dick Guldstrand for blank-check suspension work, and I was in the loop when it went to John Lingenfelter for a reliable engine capable of 200 mph. I met up with Mark in Las Vegas to help with the final preparation of the car. I took a few, tyre-warming hops in the car, and, with nearly 600 HP, I can tell you it was seriously fast. Unfortunately, on race day, the car had an oil fire in the first, six-mile straightaway, due to the headers' being a bit too close to the oil-filter canister. The required, on-board halon system saved the car and Mark and I saved what residual fun we could putting it back together and trailering it home. Later that year, Mark won a Triathlon of Motorsports hosted by a hotrodding magazine in the car, and, if I'm not mistaken, repeated the feat in '92. I have been told the car was featured on the cover of the magazine somewhere in those two years, but I have not checked that myself. I moved to Washington State and lost touch with Mark, who had a non-motorsports accident and passed away. Mark was not uniformly liked, but even his detractors will grant that he was a truly gifted driver and an engaging, entertaining, complex character. Many, currently active autocrossers will remember him. By sheer, stupid luck, I stumbled across Mark's Nevada car for sale in Florida in 1999. This is about as far away from Seattle as one can get, but the kismet was too much to ignore. I had driven this car many times in anger, had crewed it, was friends with its creator. It just had to come home to me, didn't it? Furthermore, it just HAD to run again in Nevada, didn't it? I bought the car and began the complex job of preparing it for NORC. One does not contemplate running 200 mph without giving a car a complete check-up. The energy available for destruction at 200 mph is four times the energy available at 100 mph, and sixteen times that available at 50 mph. Furthermore, the car had had an active, open-track life in the intervening years and it was time to tear it down and check it all out. You do NOT want an engine to seize or a suspension part to break at 100 mph, let alone at 200 mph. With two months to spare, it became obvious that the car would not be ready in time. Better safe than sorry, I asked the mechanics not to hurry and to make sure the car is done right. The standards for mechanical work on high-speed cars must be significantly higher than it is for road-going and autocross vehicles, for safety. The standards should be comparable to those in aviation. Hurrying is a recognized no-no in aviation, and I applied the same logic to the car work. As I write, I have an ultimate goal of running it in SCC and NORC in '01 and '02. I had already committed to run the '00 NORC, so I slapped a roll cage in my '98 Mallett 435 and went on down. This is another fabulous vehicle, but I hadn't intended to run it in high-speed events until the last minute. It was quite a hustle to get the required safety gear properly installed in time. In hindsight, I don't regret the decision. The car really came to life at NORC and I've run it in several high-speed events since then. Our flight plan called for holding speeds up to 165 for minutes at a time. As part of planning, we did a survey and calibration run of the course at legal, highway speeds. On the survey run, we noticed several bumpy spots. Driving over them at 70 mph, they were not frightening. But, we had to figure out what to expect at 165. So, right there in the middle of nowhere, we whipped out some envelopes, turned them over, pulled multicolour pens from our pocket protectors, and started scribbling. Geek racing at its best. Let us take a moment to review the goals and methods of the "back-of-the-envelope" (BOE) style of analysis introduced in Part 3 (Basic Calculations) of this series. Frequently, one simply needs a ballpark estimate or a trend. These are often much easier to get than are detailed, precise answers. In fact, they are often easy enough that they can be literally scribbled out on the backs of envelopes in the field. And that's the key point: we needed a rough idea of how the violence of the bumps varies with speed, and we needed it right then and there in the field. Another benefit of the BOE style is that it can give one a quick plausibility check on numerical data back at the lab. Thoroughgoing engineering analysis usually entails dozens of interlocking equations solved on a computer resulting in tables, plots, and charts. The intuition gets lost in the complexity. It's sometimes impossible to say, just by looking at a table or chart, whether the results are correct. On the other hand, to get our BOEs, we often make very gross approximations, such as treating the car as a rigid body; or ignoring its track width, that is, treating it as infinitely thin; or ignoring the suspension altogether; or even treating the whole car as a point mass, that is, as if all its mass were concentrated at a single point. Even so, the results are often not wildly off the numerical data, and the discrepancies can usually be explained via non-quantitative arguments. If the BOE and numerical results are wildly different, then some detective work is indicated: one or both of them is probably wrong. BOE is really a semi-quantitative oracle to the physics. These articles are about the physics of racing as opposed to the engineering of racing. We're primarily interested in the fundamental, theoretical reasons for the behaviour of racing cars. The trends and ballpark estimates we get from BOEs often do the job. Of course, this doesn't mean we won't get into more detailed treatments and computer simulation. It's just that we will always be focusing on the physics. All that said, as usual for BOE, we start with a simplistic model we can solve easily. Think of a bump in the road as a pair of matched triangles, one leading and one trailing. 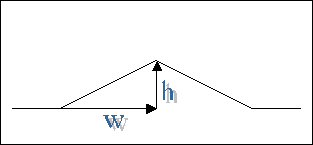
Let the width of each triangle be w and the height be h . Suppose a car approaches the bump with horizontal speed v . To assess the violence of the bump, let's ask what vertical acceleration the car will experience? If we assume a simplistic model of the car as a rigid body, we get an instantaneous, infinite acceleration right at the instant the car contacts the rising edge. We get further infinite, vertical accelerations at the two other cusps of bump the geometry. However, we know that the tyres and suspension will smooth out these sudden impulses. Calculating the effects of tyre and suspension flex is too time-consuming to do in the field even if we had data and computers on hand. However, we can get a useful approximation by assuming that the acceleration is distributed over the entire bump. If the bump is shallow (h « w) and the car is fast, then the horizontal speed doesn't change very much and the car goes up the leading edge of the bump in time t = w / v. In that time, the car goes upward a distance h, thereby acquiring a vertical speed of vy = h / t = vh / w. Since it acquires that velocity, very roughly, in time t, we can estimate the vertical acceleration to be Uh oh. BOE says that the severity of a bump goes up as the square of the speed. A bump you can feel at 50 mph is going to be sixteen times worse at 200 mph and will most definitely get your attention. The little whoopdeedoos we were noticing at 70 mph would feel (165/70)2 = 5.5 times worse at our planned speed: definitely something to anticipate on-course before we hit them. This BOE also says that the nastiness varies inversely as the width. The wider the bump, the less nasty, linearly. This is plausible. Now, let's refine the analysis a little. Conservation of energy dictates that the horizontal speed of the car must change. In our simplified, two-dimensional BOE, the velocity vector, whether on the flat or on the bump, that is, no matter what the inclination of the road. We've presupposed, here, that vertical always means "in the direction of Earth's gravitation." If we do not change the kinetic energy of the moving car, then ½ mv2 stays constant, therefore v2 stays constant. On the leading-edge ramp of the bump, remembering trigonometry, Define, as shorthand, This still varies as the square of the speed, we just take a little more time to go over the bump. The only difference to the prior formula, v2h / w, is the appearance of h2 in the denominator. Consider the case of a high, narrow bump. This case was not covered by our first BOE, which assumed that h « w. Now, with a high bump, h2 » w2 and Furthermore, of course, at constant throttle, the kinetic energy of the car will change because the force of gravitation will attenuate the vertical velocity. So, in our next consultation of the BOE oracle, we must reduce ay by The bump is getting less nasty all the time, and it's obvious that we're hitting the limitations of this BOE analysis. To expose the limitations even more starkly, consider two more questions: (1) what about the trailing edge? and (2) what about depressions, that is, down-bumps? As to the trailing edge, a simplistic car-as-rigid-body would just launch ballistically from the top of the bump. Of course, in a real car, tyre elasticity and the suspension would endeavour to keep the tyres on the ground. Short of launching, there would just be weight loss causing rebound of the tyre sidewalls and the suspension springs. Nevertheless, everyone knows that a ballistic projectile assumes a parabolic flight path, so, as long as the parabola off the top of the bump remains vertically above the down-ramp, our car-as-rigid-body is assured of taking to the air. With the simple bump geometry, we can see that a parabolic launch always starts off above the trailing-edge triangle. It intersects the road again either somewhere on the down-ramp or on the following flat bit of road, depending on horizontal speed. As to a depression - a down-bump as opposed to an up-bump - a car-as-rigid-body will simply have a ballistic phase before suffering an upward acceleration. At this point, I think we've reached the point of diminishing returns. Let us first repeat that the BOE style is doing what it's supposed to do: getting us rough trends and quantities in the field. Primarily, we wanted to find out how bump severity varies with speed, and we've got our answer: roughly quadratically. We are seeing some ways in which the model departs from intuition and reality and it's time to think about how to improve it back at the lab. The first point to notice is that we drew a pair of triangles for our bump, but used them only to calculate the time to traverse the bump and the height acquired over that time. This is not a proper dynamic analysis, in which we would use Newton's laws to model the motion of the car up and down the bump. At a glance, one can distinguish a dynamic analysis by the presence mass in the equations. Nowhere did we use the mass of the car in our BOEs above. Dynamic analysis is often too hard to do in the field because it involves integrating differential equations, almost always by computer. Another problem concerns our simplistic bump geometry. As noted above, strictly speaking, the severity of a bump on a rigid body infinite, no matter what the speed. The reason is that the car acquires its vertical component of velocity instantaneously - in zero time - upon hitting the bump, so the rate of change of the vertical velocity, that is, the vertical acceleration, is infinite at the instant the bump is encountered, then zero on the body of the up-ramp. Our list-of-things-to-do, should we wish to improve the model, includes the following tasks: Model the geometry of the bump more carefully, accounting for the fact that the initiation of the up-ramp, no matter how severe, cannot, in fact, be mathematically instantaneous. Draw some sort of little sinusoidal or exponential curves to account for the actual road profile. Integrate the equations motion of the car over the bump. Model the car more carefully, accounting for tyre flexion, springs, shocks, suspension geometry, mass distribution, moment of inertia, and all the rest. This will entail designing a suspension. These improvements put us squarely back in the lab. Ultimately, we will resort to computer simulation. As promised years ago, that is the ultimate goal of this series of articles: to spec out a simulation program. Better late than never, right? Note on Part 14, Why Smoothness The last episode of the Physics of Racing sparked a debate on reasonable values for effective wheel spring rates and raised the notion of "installation ratio." The particular point raising the debate was whether 4 Hz was a reasonable value for the resonance frequency of a real racing chassis. It seems it is certainly too fast for a road-going car, however, in the time since Part 14 was released I was introduced to a 1980 Group C Ferrari Sports Car. This is essentially a Le Mans car with a lower horsepower engine, for reliability. It is a fully aerodynamic car with ground effects that corners at 2.7g and brakes at 4g. Here's the kicker: its ride height is about half an inch, it does NOT bottom out on bumps, and its spring rate is 14,000 lb/in [sic]. I don't know the installation ratio for this car, but I would be surprised if its chassis resonance frequency was not on the order of 4 Hz or even higher. |
| Contact Sim-Racing : info (at) sim-racing.co.uk |
Sim-Racing.co.uk © 2012 - 2025 Zouq.co.uk |
 |