
|
 |
|
Why Smoothness? by Brian Beckman
I'm back after a hiatus of nine years. Time does fly, doesn't it? For those counting articles, the last one published was part 12 (Transients);
there is no Part 13.
After such a long time away, it might be worthwhile to repeat the motivation and goals of this "Physics of Racing" series. I am a physicist (the "PhD" after my name is from my Union card). I'm also an active participant in motorsports. It would be almost impossible for me not to use my professional training to analyse my hobby. So, I've been thinking for some time about the physics of racing cars. Part of the fun for me is to do totally original analyses. As such, they won't have the specifics of a hardcore engineering analysis. You can look that up in books by Fred Puhn I want the depth of understanding that can only come only from figuring things out from first principles, "peeking at the answer" from someone else's work would spoil the fun for me, I hope to give a somewhat fresh outlook on things. In 1990, one of my fellow autocrossers asked me to write a monthly column for the SCCA CalClub newsletter. After receiving lots of encouragement, I released the columns to the Internet via Team Dot Net. Back then, the Internet was really small, so I was just sharing the articles in a convenient way with other autocrossers. Since then, the Internet got big and my articles have acquired a life of their own. I have received thousands of happy-customer emails from all over the world, plus a few hate mails (mostly about article #4 (There Is No Such Thing as Centrifugal Force), in case you're wondering). So, here we go again. This month, I'd like to understand, from first principles, why it's so important to be smooth on the controls of a racing car. To me, "smooth" means avoiding jerkiness when applying or releasing the brakes, the gas, or steering. Most of the time, you want to roll on and off the gas, squeeze on and off the brakes, slither in and out of steering. It's just as important to avoid jerkiness at the end of a manoeuvre as at the beginning. For example, when steering, not only should you start turning the steering wheel with a gradual, smooth push, but you want to complete the wind-up with a gradual, smooth slowing of the push. Likewise, when you unwind the wheel, you want to start and stop the unwinding smoothly. Thus, a complete steering manoeuvre consists of four gradual, slithery start-and-stop mini-manoeuvres. A complete braking event has four little mini-slithers: one each for the start and stop of the application and the releasing of the pedal. Same for the throttle. Ok, great, but why? At first blush, it seems one would be able to get back on the gas more quickly by snapping the throttle on or get into a corner more quickly by whipping the wheel. Furthermore, supposing we can justify smoothness, are there exceptions to the rule? Are there times when it is best to snap, whip, or jerk? And exactly how smooth should one be? Smoothing means slowing the control inputs down, in a particular way, so it's obviously possible to be too smooth, as in not quick enough, as in not getting as much out of the car as it's capable of delivering. Let's tackle "why", first. As usual, physics has technical meanings for everyday words. One of the "physically correct" meanings of "smooth" is sinusoidal. A sinusoid is a curve that looks like this: 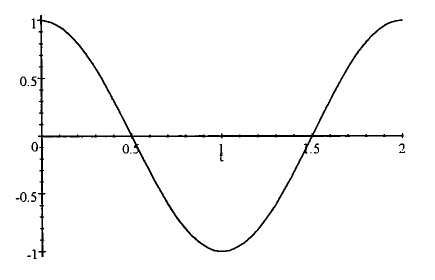 If we think of, say, steering-wheel winding angle as proportional to the vertical axis and time in seconds along the horizontal axis, then this picture describes a really smooth windup taking one second followed immediately by a really smooth unwinding taking another second. In fact, you can easily see the four mini-slithers discussed above as the head-and-tail-sections of the bumps and valleys of the curves. So, the question "why", in technical terms, amounts to asking why such a curve represents better steering input than a curve like the following, "upside-down-hat" curve: 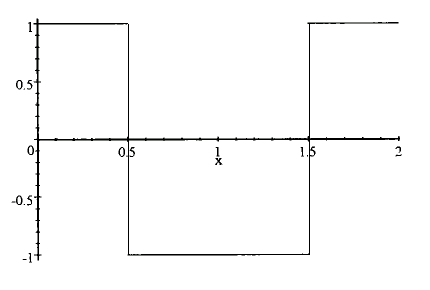 Now, here's the reason: sinusoidal inputs are better because they match the natural response of the car! The suspension and tyres perform, approximately, as damped harmonic oscillators, or DHOs. A DHO can be in one of three conditions: underdamped, critically damped, or overdamped. In the underdamped condition, a DHO doesn't have a strong damper, which is another term for shock absorber. An underdamped DHO responds sinusoidally. We've all seen cars with broken shocks bouncing up and down on the springs. In the critically damped and overdamped conditions, the car bounces just once, because the damper provides some friction to quiet down continued bouncing. However, even in these conditions, the one bounce has an approximate sinusoidal shape. The most important parameter of any DHO is its frequency. In the underdamped condition, the frequency corresponds to the number of bounces per second the DHO performs. In the critically damped and overdamped conditions--as well as in the underdamped condition, the frequency corresponds to the resonance frequency or natural frequency of the system! In other words, if you provide so many inputs per second, back and forth, as in a slalom, at the resonance frequency, the car will have maximal response. If the inputs are faster, they will be too fast for the DHO to catch up and rebound before you've reversed the inputs. If the inputs are slower, the DHO will have caught up and started either to bounce the other way or to settle, depending on condition, when the reverse input comes in. So here's the bottom line: to maximize the response of a car, you want to provide steering, braking, and throttle inputs with sinusoidal shapes at the resonance frequency of the DHOs that constitute the suspension and tyre systems. Inputs that are more jerky just dump high-frequency energy into the system that it must dissipate at lower frequencies. In other words, jerky inputs upset the car, which what drivers say all the time. By matching the shape and frequency of your control inputs to the car's natural response curve, you're telling the car to do something it can actually do. By giving the car an "instruction" like the upside-down hat, you're telling it to do something it can't physically do, so it responds by flopping and bouncing around some approximation of your input. Flopping and bouncing means not getting optimum traction; means wasting energy in suspension oscillation; means going slower. Now, there is an exception: if the front tyres are already sliding, a driver may benefit from quickly steering them into line, hoping to "catch" the car. Likewise, a jerky blip on the throttle with the clutch engaged to bring up the revs to match the gears on a downshift is usually the right thing to do. But, when the car is hooked up, getting the most out of the car means simulating the response of the various DHOs in the system with steering, braking, and throttle inputs. Now we know the physics behind it. Let's do some math! The frequency turns out to be 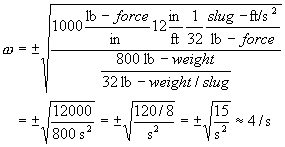 Notice that we've used the back-of-the-envelope style of computation discussed in part 3 (Basic Calculations) of this series. We've found that the resonance frequency of one corner of a car is about 4 bounces per second! This matches our intuitions and experiences: if one pushes down on the corner of a car with broken shocks, it will bounce up and down a few times a second, not very quickly, not very slowly. We can also see that the frequency varies as the square root of the spring constant. That means that to double the frequency, say, to 8 bounces per second, we must quadruple the spring strength to 4,000 lb/in or quarter the sprung weight to 200 lb. [Note added in proof: My friend, Brad Haase, has pointed out that 4 Hz, while in the "ballpark", is much too fast for a real car. Now, this series of articles is only about fundamental theory and ballpark estimates. Nonetheless, he wrote convincingly "can you imagine a 4-Hz slalom?" I have to admit that 4 Hz seemed too fast to me when I first wrote this article, but I was unable to account for the discrepancy. Brad pointed out that the suspension linkages supply leverage that reduces the effective spring rate and cited the topic "installation ratio" in Milliken's book Race Car Vehicle Dynamics How do we derive the frequency formula? Let's work up a sequence of approximations in stages. By improving the approximations gradually, we can check the more advanced approximations for mistakes: they shouldn't be too far off the simple approximations. In the first approximation, ignore the damper, giving us a mass block of sprung weight resting on a spring. This model should act like a corner of a car with a broken shock. Let the mass of the block be m. The force of gravitation acts downwards on the block with a magnitude mg, where g = 32.1 ft/s2 is the acceleration of Earth's gravity. The force of the spring acts upward on the mass with a magnitude k(y0 - y), where k is the spring constant and (y - y0) is the height of the spring above its resting height y0 (the force term is positive--that is, upward--when y - y0 is negative--that is, when the mass has compressed the spring and the spring pushes back upwards). We can avoid schlepping y0 around our math by simply defining our coordinate system so that y0 = 0. This sort of trick is very useful in all kinds of physics, even the most advanced. It's worth noting that the model so far ignores not only the damper, but the weight of the wheel and tyre and the spring itself. The weight of the wheel and tyre is called the unsprung weight. The weight of the spring itself is partially sprung. We don't add these effects in the current article. Today, we stop with just adding the damper back in, below. Newton's first law guides us from this point on. The total force on the mass is -ky - mg. The mass times the acceleration is m (dvy / dt) = m (d2y / dt2), where vy is the up-and-down velocity of the mass and dvy / dt is the rate of change of that velocity. That velocity is, in turn, the rate of change of the y coordinate of the mass block, that is, vy = (dy / dt). So, the acceleration is the second rate of change of y, and we write it as d2y / dt2 because that's the way Newton and Leibniz first wrote it 350 years ago. We have the following dynamic equation for the motion of our mass block. Let's divide the entire equation by m and rearrange it so all the terms are on the left: If we're careful about units, in particular about slugs and lbs (see article 1 - Weight Transfer), then we can note that k/m has the dimensions of 1/sec2, which is a frequency squared. Let's define yielding We need to solve this equation for y(t) as a function of time t. To follow the rest of this, you'll need to know a little freshman calculus. Take, as ansatz, then and therefore 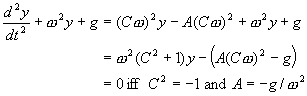 So, we see there are two solutions, Let's get out of the complex domain by writing 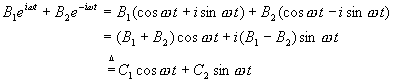 This definition makes our initial conditions simpler, too: It's easy, now, to add the damper. Damping forces are proportional to the velocity; that is, there is no damping force when things aren't moving. Each corner approximately obeys the equation where where then and therefore 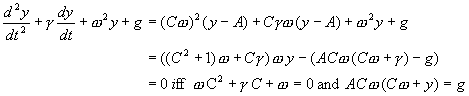 You may remember the little high-school formula and I'll leave the simple arithmetic for A and the initial conditions to the reader. The critically damped condition obtains when It will be fun and easy for anyone who has followed along this far to plot out some curves and check out my math. If you find a mistake, please do let me know (I just wrote this off the top of my head, as I always do with these articles). We could improve the approximation by writing down the coupled equations, that is, treating all four corners of the car together, but that would just be a lot more math without changing the basic physics that the car responds more predictably to smooth inputs and less predictably to jerky inputs. Another improvement would be to add in the effect of the unsprung and partially sprung weight. |
| Contact Sim-Racing : info (at) sim-racing.co.uk |
Sim-Racing.co.uk © 2012 - 2025 Zouq.co.uk |
 |