The goal in this and the next instalment of the Physics of Racing is to combine the magic formulae of
The Magic Formula: Longitudinal Version
and
The Magic Formula: Lateral Version, so that we
have a model of tyre forces when turning and braking or turning and accelerating at the same time. In this part, we figure out
combination slip, and in the next instalment, we figure out
combination grip. Roughly speaking,
slip is the input and grip is the output to our model. Slip comes from control inputs on brakes, throttle and wheel, grip comes from
reaction forces of the ground on the tyres.
The regular magic formulae apply only to a tyre generating longitudinal or lateral forces in isolation, that is, to a tyre
accelerating or braking and not turning, or a tyre turning but not accelerating or braking. In
The Traction Budget, we approximated the response
under combination slip by noting that it follows the circle of traction. A tyre cannot deliver maximal longitudinal grip when it's
delivering lateral grip at the same time, and vice versa. According to my sources, modelling of combination slip and grip is an area
of active research, which means we are on our own, once again, in the original, risk-taking spirit of the Physics of Racing series.
In other words, we're going way out on a limb and this could all be totally wrong, but I promise you lots of fun physics on the
journey.
From
The Magic Formula: Longitudinal Version, recall our definition for the longitudinal slip,
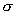
, the
input to the longitudinal magic formula
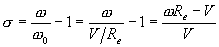
where V is the forward speed of the hub w.r.t. ground, Re is a constant, the effective radius, for a given tyre, and
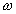
Re
is the backward speed of the CP w.r.t. the hub. Therefore,
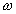
Re - V is the
backward speed of the CP w.r.t. EARTH. A slick technique for proving this, and, in fact, for figuring out any combinations of
relative velocities (
Space, Time, and Rubber) is as follows.
Write V = HUB - GD, meaning speed of the HUB relative to the ground (GD). Now write
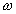
Re
= -(CP - HUB) meaning the backward speed of the CP relative to the HUB; the overall minus sign outside reminds us that we want
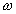
Re
positive when the CP moves backwards w.r.t. the hub. Now, just do arithmetic:
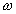 Re- V = -(CP - HUB) - (HUB - GD)
=-CP + HUB - HUB + GD = -(CP - GD)
Re- V = -(CP - HUB) - (HUB - GD)
=-CP + HUB - HUB + GD = -(CP - GD)
voila, backward speed of the CP w.r.t. the ground. This realization gives us intuition into the sign of
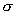
:
if and only if the CP moves backwards faster than the hub moves forward; the car accelerates forward-visualize that in your head; in
that case,
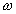
Re is greater than V;
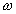
Re-
V is greater than zero; and is positive.
It turns out that we developed this formula only for the case when V is positive, that is, the car is moving forward. And, in fact,
the formula only works in that case. To generalize it to cars moving in reverse, we'd best analyse it in excruciating detail. A
moment's reflection reveals that there are eight cases: two signs for V, two signs for
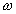
Re, and two cases for whether the absolute
value of V is greater than the absolute value of Re, yielding eight = (2
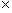
2
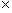
2) p
ossibilities, which have the following physical interpretations:
- Car (hub) moving forward, CP moving slowly forward w.r.t. ground, resisting car motion. This models driving slowly in reverse gear
while moving forward. Slowly, here, means slowly relative to V, or, precisely, that
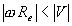 , where
, where 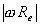 is the absolute value or unsigned magnitude of
is the absolute value or unsigned magnitude of 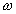 Re and
Re and 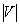 is the absolute value or unsigned magnitude of V.
is the absolute value or unsigned magnitude of V.
- Same as above, just with CP moving quickly forward, that is with
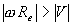 .
.
- Car moving forward, CP moving slowly backwards, just not quickly enough to accelerate the car. This is braking or engine braking in
forward gear. Wheel lockup while moving forward falls in this case, too.
- Car moving forward, CP moving quickly backwards, accelerating the car forward.
- Car moving backward, CP moving slowly forwards, just not quickly enough to accelerate the car backward. This is braking or engine
braking in reverse, and wheel lockup in reverse falls in this case.
- Car moving backward, CP moving quickly forward, accelerating in reverse.
- Car moving backward, CP moving slowly backward, resisting motion.
- Car moving backward, CP moving quickly backward, resisting motion.
We've caught all this in the following diagram, in which we have drawn V and
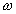
Re as arrows, pointing in the actual direction that the
hub moves w.r.t. the ground and the CP moves w.r.t. the hub, respectively. Algebraically, V and
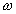
Re
have opposing sign conventions, so
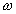
Re is negative when its arrow points up. In
looking at this table, note that the longitudinal force Fx has the same sign as
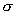
.
When Fx and are positive, the car is being forced forward by the ground's reacting to the tyres. When they're negative, the car is
being forced backwards. So, to figure out which way the car is being forced, just look at the sign of
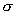
.
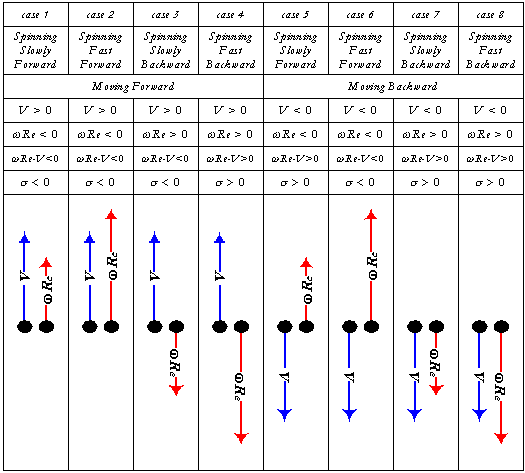
Inspection of this table reveals that the following new formula works in all cases:
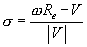
Where the numerator,
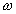
Re - V is the signed difference of the two speeds and the
denominator is unsigned. It is perhaps surprising that there is so much richness in such a little formula. However, it is precisely
this richness that we must maintain as we add steering, that is, lateral slip angle at the same time. The best way to do that is to
vectorize the formula so that the algebraic signs of the vector components take the place of the signed quantities V and
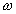
Re. The approach here parallels the approaches of
RARS,
A Simple Racing Simulator and
Space, Time, and Rubber. We want the signed
component Vx to take the place of the old
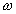
, signed V, the signed component Lx of
the slip velocity L to take the place of the old Re, and V now to denote the unsigned magnitude of the vector V, that is
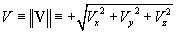
.
The next table summarizes these changes:
|
Quantity
|
old notation
|
new notation
|
vector
|
|
signed, forward speed of hub w.r.t. EARTH
|
V |
Vx
|
V
|
|
signed, backward speed of CP w.r.t. hub
|
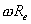
|
-Wx
|
W
|
|
unsigned magnitude of hub speed
|
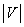
|
V
|
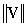 or V or V
|
|
signed, backward speed of CP w.r.t. EARTH
|
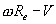
|
-Lx
|
L = V + W
|
|
signed, longitudinal slip
|
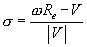
|
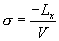
|
?
|
Slip velocity, L [Lx, Ly, Lz] = V + W is the plain-old vector velocity of the CP w.r.t. EARTH with no secret sign convention to
confuse things. As an aside, we note that when the car sticks to the ground on flat road, we may assume Lz = 0. W is CP velocity
w.r.t. hub. In the TYRE system, W has only a (signed) x-component, that is, WTYRE = [Wx, 0, 0]. These definitions hold whether the
car is moving forward or backward, accelerating or braking.
The big question mark in the table indicates that we do not have a vector for combination slip because we measure its longitudinal
and lateral components differently, as a ratio and as an angle, respectively. Note that, since lateral slip is the angle made by V
in the TYRE system, it is
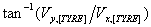
. Since L = V + W, it's easy to see
that
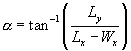
which is a most convenient expression, though some attention must be paid to the quadrant in which the angle falls. We resolve this
in the next two instalments of PhORS as we stitch together the two magic formulae to make
Combination Grip.
But first, let's update the big diagram, showing all eight cases with a little slip angle thrown into the mix, and the vector sum,
L = V + W, replacing the ad hoc, signed quantities of the old notation. The sign of the slip angle
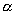
does not introduce new cases so long as
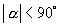
because the right-hand
and left-hand cases are precisely symmetrical. The nice thing, here, is that we can treat all eight cases the same way-the nature of
vector math takes care of it because the magnitude of a vector is always unsigned. Using signed, scalar quantities, we had to dissect
the system and introduce absolute value to get everything to work. Absolute value has always struck me as a kind of crock or kludge
to use when the math is just not sufficiently expressive. The main contribution of this instalment is to fix that problem.



